一、欧几里得算法(辗转相除法)
首先我们要知道,初等数论中: 若(p,q)=1,存在整数s,t 使得sp+ tq=1 (x,y)表示x,y的最大公约数 [x,y]表示x,y的最小公倍数
先举个例子:
gcd(6,16) = gcd(16,6%16) = gcd(16, 6) = gcd(6,16%6) = gcd(6,4) = gcd(4,6%4) = gcd(4,2) = gcd(2,4%2) = gcd(2,0) = 2
由此可得,欧几里得算法就是计算最大公约数的一个算法,递推式为:
gcd(a , b)= gcd(b , a % b)
直到a,b中有一个数为0,可得到他们的最大公约数。 怎么证明上述式子呢?` 令(A , B) = R,证明(A,B) = (B,R)
因 (A , B) = R 则 A = B * q + R 令 A = a * u, B = b * u 则 R = A - B*q = a * u - b * u * q = u * (a - b * q) = u * n 即 u 是A,B的最大公因数则 u 是B,R的最大公因数. 同理: 令 B = b' * v 令 R = r' * v 得 A = a' * v 即 v 是B,R的最大公因数则 v 是A,B的最大公因数. 证明成立
二、裴蜀定理
内容如下:
\(若 a , b 是任意整数,且 gcd ( a , b ) = d ,那么对于任意的整数 x , y , a x + b y 都一定是 d 的倍数,特别地,一定存在整数 x , y,使 a x + b y = d 成立。\)
推论:
a,b互质的充分必要条件是存在整数x,y使ax+by=1 假设我们有一个关于x和y的线性方程 ax + by = d,现在要求判断这个方程是否存在整数解。
裴蜀定理告诉我们,ax + by = d存在整数解当前仅当 gcd ( a , b ) | d 。例如说3x + 6y = 2就不存在整数解,3x + 6y = 3就存在整数解 x =1 ,y = 0 。
如何证明?显然gcd( a , b) | (ax + by),如果存在整数的解的话必然有 gcd ( a , b ) | d 。
那么在gcd( a, b) | d的时候一定都存在整数解吗?我们来通过扩展欧几里得算法解释这个问题,实际上,扩展欧几里得的算法不仅回答了这个问题,而且还把解构造了出来。
n个整数的裴蜀定理:
设a1,a2,a3......an为n个整数,d是它们的最大公约数,那么存在整数x1......xn使得x1a1+x2a2+...xn*an=d。 特别来说,如果a1...an存在任意两个数是互质的(不必满足两两互质),那么存在整数x1......xn使得x1 * a1 + x2 * a2+...xn * an=1。证法类似两个数的情况。
三、扩展欧几里得算法
定义: 在得到整数a,b的最大公约数后,还希望得到整数x,y:使得ax+by=gcd(a,b)
1、\(对于整数a>b显然b=0时,gcd(a,b) = a;此时x=1,y=0\)
2、\(设ax_1+by_1=gcd(a,b)\)
3、\(有bx_2 + (a\%b)y_2=gcd(b,a\%b)\)
4、\(由于gcd(a,b)=gcd(b,a\%b),那么ax_1+by_1=bx_2+(a\%b)y_2\)
5、\(即ax_1+by_1=bx_2+(a-[a/b]*b)y_2=ay_2+bx_2-[a/b]*by_2\)
6、\(也就是ax_1+by_1==ay_2+b(x_2-[a/b]*y_2)\)
7、\(根据恒等式定理得:x_1=y_2;y_1=x_2-[a/b]*y_2\)
8、\(这样我们就得到了求解x_1,y_1的方法:x_1,y_1的值基于x_2,y_2\)
9、上面的思想是以递归定义的,gcd不断地递归求解一定会有b=0的时候,所以递归可以结束.
四、扩展欧几里得算法求逆元
乘法逆元的定义: 若存在正整数a,b,p, 满足ab = 1(mod p), 则称a 是b 的乘法逆元, 或称b 是a 的乘法逆元。b ≡ a-1 (mod p),a ≡ b-1 (mod p)
比如说, 在模7 意义下,3 的乘法逆元是5, 也可以说模7 意义下5的乘法逆元是3。模13意义下5的逆元是8……
存在性 看起来和同余方程很相似(其实下面真的可以用exgcd求的!),在同余方程中, ab ≡ 1(mod p) 若a 与p 互质, 则一定存在一个正整数解b, 满足b < p,若a 与p 不互质, 则一定不存在正整数解b. 所以逆元要求a与p互质 定义函数
def exgcd(a,b):
global x,y
if b == 0:
x,y = 1,0
return a
d = exgcd(b,a%b)
x,y = y,x
y -= (a//b)*x
return d
用gmpy2库
gmpy2.is_prime(n) # 判断n是不是素数
gmpy2.gcd(a,b) # 欧几里得算法
gmpy2.gcdext(a,b) # 扩展欧几里得算法
说明:gmpy2.gcdext(a,b)返回一个元组(g,s,t) , g =gcd(a,b) , g=as+bt
import gmpy2
print(*map(int,gmpy2.gcdext(15,10)))
输出:
5 1 -1 #即gcd(15,10) = 5 = 1*15+(-1)*10
五、中国剩余定理
例1、求满足下同余方程组的x
\(\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\Updownarrow\)等价
则可以知道 3,5,7|(x+2) \(\Rightarrow\) 105|(x+2) \(\Rightarrow\) x=103、103+105\(\cdots\) 即x最小值为103。
例2、
可以先寻找满足以下条件的方程组 (可看作基础解系)
则式2.1记为 \(k=ax+by+cz \quad (mod \quad 105)\)
由基础解系知道:35|x,21|y,15|z
x = 35t-1=3s,即存在整数s,t使得35t-3s=1
可以得出一组解:
即:\(k=70a+21b+15c(mod \quad105)\),余数就是k的值
根据上述再求例1
\(x = 70*1+21*3+15*5 (mod\quad105)=208\quad mod \quad105=103。\)
用现代数学的语言说明,中国剩余定理给出了以下的一元线性同余方程组:
整数\(m_1\)、\(m_2\)\(\cdots\)\(m_n\)两两互质,则对任意的整数\(a_1\)、\(a_2\)\(\cdots\)\(a_n\)方程组(S)有解;
\(x=a_1y_1+a_2y_2+\cdots+a_ny_n(mod \quad m_1m_2\cdots m_n)\)
其中\(y_1=(m_2\cdots m_n)t-1=m_1s\),因为\((m1,m_2\cdots m_n)=1\),满足条件的整数s,t一定存在。
六、中国剩余定理拓展
中国剩余定理要求模数两两互质,而一般情况下我们要解决的都是\(m_i\)不互质问题,这就推广到中国剩余定理的拓展!
从只含有两个的方程的同余方程组开始
等价于
消去x后得
因为模数不是两两互质,这个方程是否存在整数解就需要考虑一下。根据裴蜀定理,我们可以知道如果\(gcd(m_1,m_2)|(a_1,a_2)\)那么这个方程一定有整数解,否则不存在整数解。
当它存在整数解的时,假设我们已经根据扩展欧几里得算法求得一组特殊解\((k_1',k_2')\),将任意一个解回代到(1)中,就会得到满足同余方程组的解,记\(x_0\)。
由此推出所有解:
我们设\(g = gcd(m_1,m_2)\),又由于\(a_2-a_1\)是\(g\)的倍数,那么可以把方程(1)改写为 $$ k_1\frac{m_1}{g}-k_2\frac{m_2}{g}=\frac{a_2-a_1}{g}\tag3 $$
这样的话,\(\frac{m_1}{g}和\frac{m_2}{g}就互质了\),那么这个方程所有整数解就是
这里的t是任意整数。 往回代入可以得到
这个解等价于同余方程
$$ z\equiv x_0(mod \quad lcm(m_1,m_2)) $$
由此得出,更完整的中国剩余定理
对于一个同余方程组
它等价于
$$ x\equiv x_0(mod\quad lcm(m_1,m_2,\cdots,m_n)) $$
这里\(x_0\)是这个方程的任意解,可以通过刚才的合并计算得到。
十三届蓝桥杯习题:
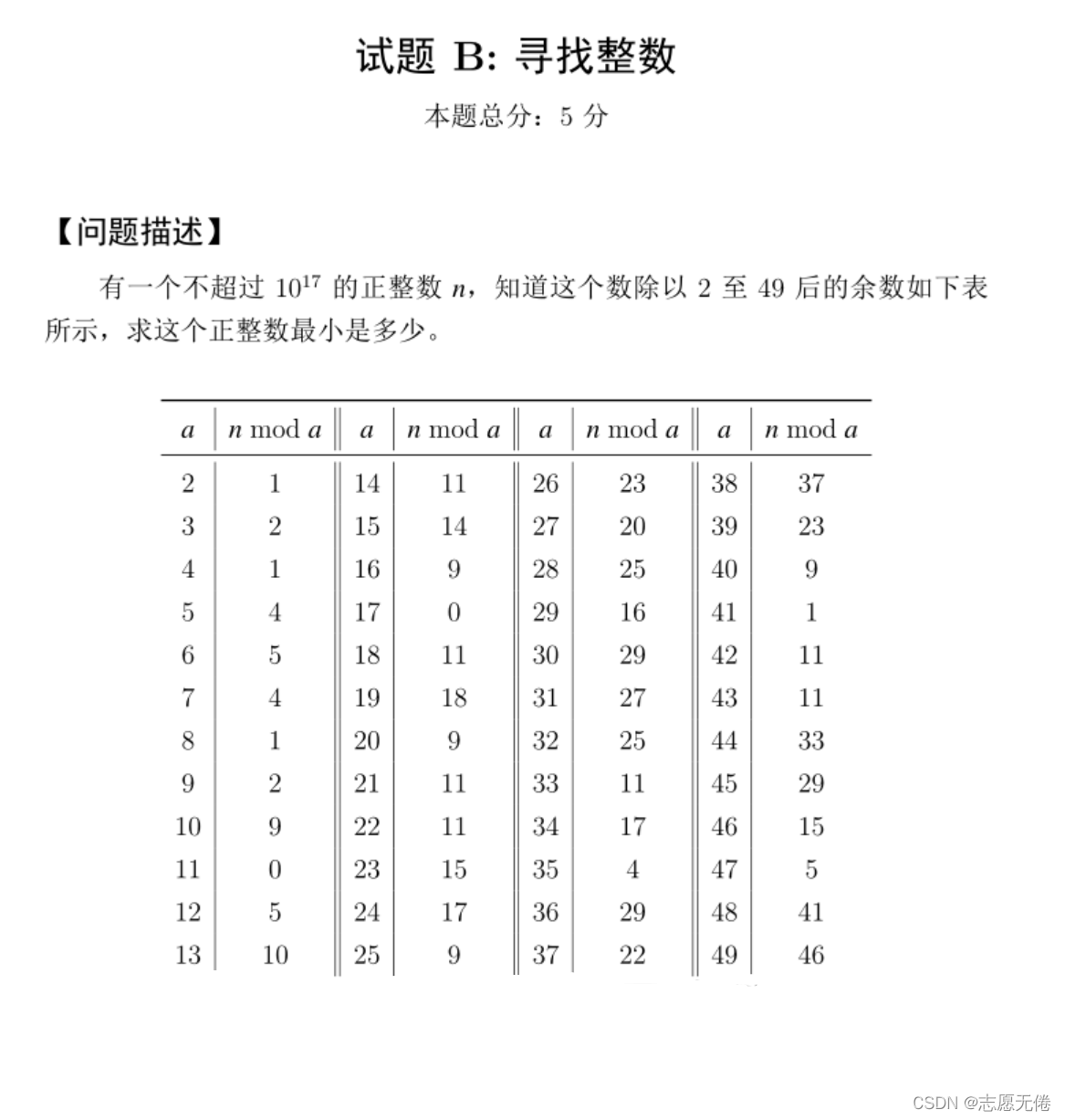
方法1(暴力): 用后面的数找规律,得等差数列,再遍历满足前面条件参考
方法2:中国剩余定理
math.lcm求最小公倍数,math.gcd求最大公约数
print(math.lcm(8,41,16))
最大公约数记为(a,b),最小公倍数记为[a,b]
import math
from functools import reduce
from sympy import rem
import gmpy2
a = [1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
l = []
for i in range(len(a)):
l.append(i+2)
def zhi(x):
for i in range(2,int(x**0.5+1)):
if x%i==0:
return False
else:
return True
mod_num = []
rem_num = []
for i in range(len(a)):
if zhi(l[i]):
mod_num.append(l[i])
rem_num.append(a[i])
else:
continue
print(mod_num)
print(rem_num)
M = reduce(lambda x,y:x*y,mod_num)
Mm = []
y = 0
for i in range(len(mod_num)):
t = M//mod_num[i]
_,a,_ = gmpy2.gcdext(t,mod_num[i])
Mm.append(int(a%mod_num[i]))
y += (t*Mm[i]*rem_num[i])
print(y%M)
输出:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
[1, 2, 4, 4, 0, 10, 0, 18, 15, 16, 27, 22, 1, 11, 5]
2022040920220409
方法3:中国剩余定理拓展
a = [1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
l = []
for i in range(len(a)):
l.append((i+2,a[i]))
def exgcd(a, b):
global k1, k2
if b == 0:
k1, k2 = 1, 0
return a
d = exgcd(b, a % b)
k1, k2 = k2, k1
k2 -= (a // b) * k1
return d
m1 = l[0][0]
b1 = l[0][1]
flag = 0
for i in range(1,len(l)):
m2 = l[i][0]
b2 = l[i][1]
k1,k2 = 0,0
d = exgcd(m1,m2)
if (b2-b1)%d:
flag = 1
break
k1 *= (b2-b1)//d
# k1' = k1 + k * (m2 // d) , k取任意整数
t = m2//d
k1 = k1%t #取最小的k1
# x = b + km
b1 = k1*m1+b1
m1 = m1//d*m2
if flag:
print(-1)
else:
print(b1%m1) #x的最小整数解
输出:
2022040920220409