层次分析法
层次分析法(AHP)是由美国运筹学家、匹兹堡大学教授T.L.Saaty于20世纪70年代创立的一种综合评价方法。其本质是一种分解复杂问题的过程。该过程结合了人类决策时的基本步骤,即分解、判断、综合。在一定程度上减少了决策者的主观性。
基本步骤
- 分析系统中各因素之间的关系,建立系统层次结构。
- 对同一层次中的各个元素进行两两比较,构建比较矩阵。
- 计算各层次比较矩阵中各元素的相对权重,对比较矩阵的一致性进行检验。
- 计算整个系统下的合成权重,并计算被评价对象的总分。
所谓层次结构就是层次分析法需要将决策分解成目标层O、准则层C、方案层P这三个层次。
以挑选美食为例,通过建立层次分析模型的方法挑选出对你来说最好的食物。
因此第一步,三个层次自上到下,如该层次结构图:
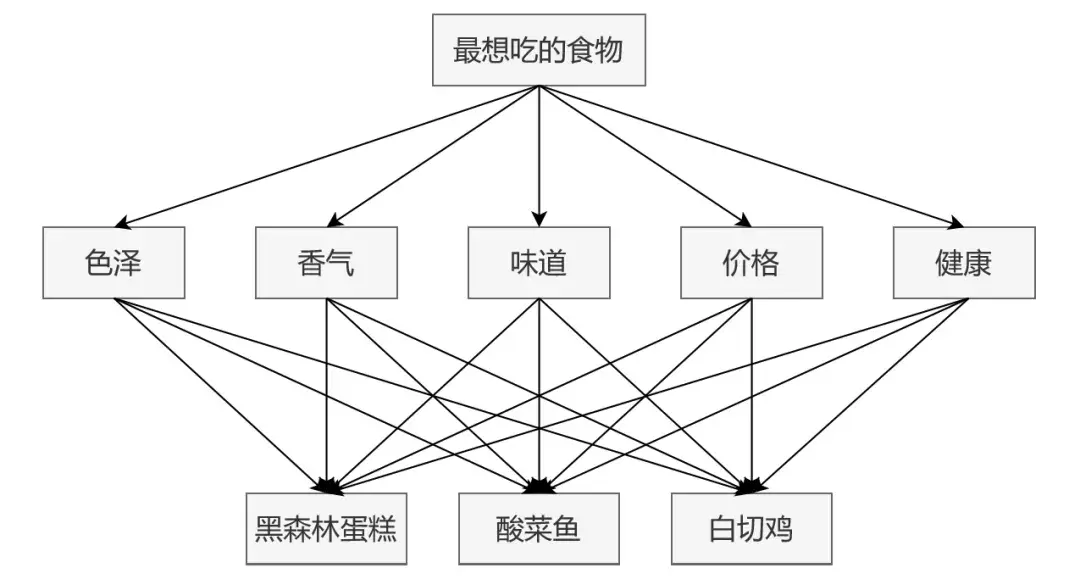
第二步建立准则层的比较矩阵:
注意:准则层(一个)和方案层(五个)的比较矩阵都需要构建。
其中准则层的比较矩阵如下:

然后就是方案层的比较矩阵,以色泽为例,如下:
| 色泽 | 黑森林蛋糕 | 酸菜鱼 | 白切鸡 |
|---|---|---|---|
| 黑森林蛋糕 | 1.00 | 2.00 | 5.00 |
| 酸菜鱼 | 0.50 | 1.00 | 2.00 |
| 白切鸡 | 0.20 | 0.50 | 1.00 |
准则层比较矩阵A,其中\(a_{ij}\)代表第i行对应准则的重要程度是第j列对应准则的重要程度的\(a_{ij}\)倍。例上述准则层比较矩阵中的4,代表色泽重要程度是味道的4倍。
方案层比较矩阵B,其中\(b_{ij}\)代表第i行对应方案的得分是第j列对应方案的得分的\(b_{ij}\)倍。例上述方案层比较矩阵中的5,代表色泽方面,黑森林蛋糕的得分是白切鸡的5倍。
对于重要性标度,Saaty等人提出1~9尺度,\(a_{ij}\)取值1,2,...,9及其互反数1,1/2,...,1/9
一般依照下表:
| 尺度\(a_{ij}\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 准则\(C_i:C_j\)的重要性 | 相同 | 介于之间 | 稍强 | 介于之间 | 强 | 介于之间 | 明显强 | 介于之间 | 绝对强 |
第三步分别计算准则层和方案层各要素的权重
我们以准则层为例,知道判断矩阵A如下:
一般有三种求权重的方法:
- 算数平均权重
- 几何平均权重
- 特征值求权重
一般采用第三种方法求权向量,比赛可以都写上。
具体公式参考
进行一致性检验
由于判断矩阵最大特征根\(\lambda_{max}\)的特征向量,经归一化(使向量中各元素之和等于1)后记为W。而能否将该特征向量作为各指标的权向量,需要进行一致性检验,若通过,则得到的W合理。
由于λ连续的依赖于\(a_{ij}\),则λ比n大的越多,A的不一致性越严重,一致性指标用CI计算,CI越小,说明一致性越大。用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量,其不一致程度越大,引起的判断误差越大。因而可以用 λ-n 数值的大小来衡量A 的不一致程度。定义一致性指标为:
CI=0,有完全的一致性;CI 接近于0,有满意的一致性;CI 越大,不一致越严重。
为衡量CI的大小,引入随机一致性指标RI:
随机一致性指标RI与判读矩阵的阶数有关,一般情况下,矩阵阶数越大,则出现一致性随机偏离的可能性也越大,其对应关系如下:
| 矩阵阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
然后得出检验系数:
一般,如果CR<0.1 ,则认为该判断矩阵通过一致性检验,否则就不具有满意一致性。
用相同的方法可以求出方案层(五个)的权重,记为各个方案在不同准则下的得分,组合得到一个5×3的矩阵。最终再对应乘以准则权重,求和记为各个方案的最终得分。
代码如下
import numpy as np
# 随机一致性指标RI
RI_dict = {1: 0, 2: 0, 3: 0.58, 4: 0.90, 5: 1.12, 6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45}
#比较矩阵(正互反阵)
A = [[1, 1/2, 4, 3, 3],
[2, 1, 7, 5, 5],
[1/4, 1/7, 1, 1/2, 1/3],
[1/3, 1/5, 2, 1, 1],
[1/3, 1/5, 3, 1, 1]]
n = len(A)
#由A确定五个准则C对目标层的权重
#算数平均法求权重
def ssa(A,n):
sum_A = np.sum(A,axis=0,keepdims=True)
w = np.sum(A/sum_A,axis=1)/n
return w
#几何平均法求权重
def jha(A,n):
mul = np.prod(A,axis=1)
fz = mul**(1/n)
w = fz/np.sum(fz)
return w
#特征值法求权重
def tzz(A,n):
V,D = np.linalg.eig(A) #V是特征值,D是特征向量,每一列是一个特征向量
maxv = np.max(V) #最大特征值
c = np.where(V==maxv) #返回maxv所在的行和列
b = D[:,c[0]] #找到最大特征值对应特征向量
w = b/sum(b)
return np.squeeze(w) #删除数组形状中的单维度
V,D = np.linalg.eig(A)
maxv = np.max(V)
CI = (maxv-n)/(n-1) #一致性指标
RI = RI_dict[n] #随机一致性指标
CR = CI/RI #一致性比率
if CR<0.1:
print(f'检验系数为:{CR},一致性检验通过')
print(tzz(A,n))
else:
print(f'检验系数为:{CR},一致性检验未通过')